発表のポイント:
- 植物の葉の原基(注1)が発生する際の制御に関して考えられていた基本的な枠組みの一部を見直し、葉の配列(葉序(注2))に見られる規則的なパターンのほとんど全てを再現できる抽象モデルを構築しました。
- 対称性をもたないコクサギ型葉序(注3)の出現など、葉序に残されていた問題のいくつかを解決するとともに、葉原基の発生制御における原基間作用の時間変化の重要性を明らかにしました。
- 自然が織りなす美しい幾何学的パターンを、生成原理から解き明かすことにつながると期待されます
概要:
植物の葉の原基は茎頂の分裂組織(注4)の周縁部に発生し、茎の周りに葉序と呼ばれる規則的な配列パターンを描いていきます。多くの植物では葉序はらせん対称(注5)か放射対称であり、二列互生(注6)、フィボナッチらせん(注7)(開度(注8)が黄金角(注9)に近いらせん)、十字対生(注10)、三輪生(注11)のいずれかのパターンを取ります。これら主要な葉序については、既存の葉原基が発する原基形成抑制力の影響を避けるように新しい原基が生じる、と考える抑制場モデルで説明されていました。しかし、従来のモデルでは説明のつかない葉序もありました。その代表例が、対称性をもたず、開度が180°→90°→180°→270°と周期的に変化する、コクサギ型葉序です。東京大学大学院理学系研究科の米倉崇晃大学院生と杉山宗隆准教授、神奈川大学の岩元明敏准教授(研究当時は東京学芸大学)、アストロバイオロジーセンター・基礎生物学研究所の藤田浩徳助教らのグループは、抑制力の原基齢依存的な変化を導入して抑制場モデルを拡張することで、コクサギ型葉序の再現に成功し、さらにこの拡張モデルが他の点でも従来モデルより実際の葉序によく合致することを明らかにしました。今回の結果は原基間作用の時間変化の重要性を示し、葉序の本質的理解に寄与するものであり、自然が織りなす美しい幾何学的パターンを、生成原理から解き明かすことにつながると期待されます。
発表内容:
植物の葉が茎の周りに描く配列の様式を葉序と言います。ほとんどの植物で葉序はある種の数学的規則を満たすらせん対称性か放射対称性を示し、その大半が二列互生、フィボナッチらせん(開度が黄金角に近いらせん)、十字対生、三輪生のいずれかのパターンを取っています。こうした葉序パターンに見られる規則性の不思議さは、古くから人々の興味を掻き立て、様々な研究を生んできました。葉序のパターンは葉の相互の位置関係にほかならず、その根本は葉の発生制御にあります。19世紀にはすでに形態学的観察から、新しい葉の原基が茎頂の分裂組織の周縁部に発生するときに、先行する葉原基からの距離を最大にする位置を選んでいるように見えることが指摘されていました。その後、先行原基からの原基形成抑制作用の影響下で新たな原基の発生位置が決定し、それが葉序のパターンを形づくっていく、と考えられるようになり、この考えに基づいて葉序を説明しようとする数理モデルが数多く提案されました。中でも特筆すべきものに DouadyとCouderによる2つの抑制場モデル、互生葉序に特化したDC1と葉序全般を扱えるDC2があります。
DC1とDC2はともに、各葉原基が一定の原基形成抑制力を発しており、その作用が距離に応じて減衰することを仮定しており、これに加えてDC1は、決められた時間ごとに分裂組織周縁部で先行原基からの抑制作用の総和が最も低い地点に一つずつ新しい原基が発生することを、またDC2は、分裂組織周縁部に先行原基からの抑制作用の総和がある閾値を下回る地点が現れると、直ちにそこに新しい原基が発生することを仮定しています。DouadyとCouderは、DC1を用いたコンピュータシミュレーションではパラメータの設定次第で二列互生やフィボナッチらせんが生成すること、DC2を用いたシミュレーションでは主要な葉序パターン4種のどれもが生成することを示し、これによって先行原基による新たな原基形成の抑制が葉序の決め手であることを明らかにしました。この抑制作用はDCモデルでは仮想的なものでしたが、近年の生理学的・分子生物学的な解析から、新たな葉原基の発生に植物ホルモンのオーキシンが必須であることや、先行原基が周囲からオーキシンを吸収していることがわかり、オーキシン収奪として抑制作用の実体を捉えられるようになりました。このような一連の研究を受けて、現在ではDCモデルが想定した葉原基発生制御の枠組みが葉序のパターン形成の基本機構として広く受け入れられるに至っています。

コクサギの枝と冬芽。冬芽は、P3以前の葉原基を取り除いてから、走査型電子顕微鏡で観察した(Oは茎頂分裂組織の中心、Pは葉原基で添えた数字が小さいほど若い)。開度が周期的に変化する互生という、コクサギ型葉序の特徴が見て取れる。
しかし、DCモデルで全ての葉序パターンに説明がついたかというとそうではなく、説明されないままとなっていた葉序もありました。その代表例が、らせん対称性も放射対称性ももたず、開度が180°→90°→180°→270°と周期的に変化する、コクサギ型葉序です。コクサギ型葉序は、ムクロジ目ミカン科のコクサギ(図1)のほか、キジカクシ目ツルボラン科のシャグマユリなど、少数ながら様々な分類群に散見されることから、葉原基の発生制御の枠組み自体が特殊化したためにコクサギ型となったわけではなく、共通の枠組みが特定の条件でコクサギ型を生み出すと推察されます。そうであれば、従来のモデルがコクサギ型葉序を生成できないのは、モデルの想定に不備があることを意味します。
東京大学大学院理学系研究科附属植物園の米倉崇晃大学院生と杉山宗隆准教授、神奈川大学理学部の岩元明敏准教授(研究当時は東京学芸大学教育学部)、アストロバイオロジーセンター・基礎生物学研究所の藤田浩徳助教らのグループは、上記の考えに立って葉原基発生制御の枠組みを見直し、コクサギ型葉序を含む、ほぼ全ての葉序パターンを生成できるよう、DCモデルの拡張を試みました。着目したのは、葉原基が発する原基形成抑制力です。これは従来のモデルでは、原基が出現した瞬間から一定の強さであるとされていましたが、生物学的にはむしろ不自然な仮定です。そこで、この抑制力に原基齢に依存した時間変化を導入し、DC1を拡張したEDC1とDC2を拡張したEDC2を構築しました。これらのモデルを用いて徹底的なコンピュータシミュレーションを行った結果、EDC2において抑制力がゆっくりと上昇するときに、特定のパラメータ条件でコクサギ型葉序のパターンが生成しました(図2)。このコクサギ型葉序はパラメータ空間(注12)の中でフィボナッチらせんや十字対生と近接しており、境界部ではわずかなパラメータの変化で生成パターンの対称性が現れたり失われたりすることもわかりました。
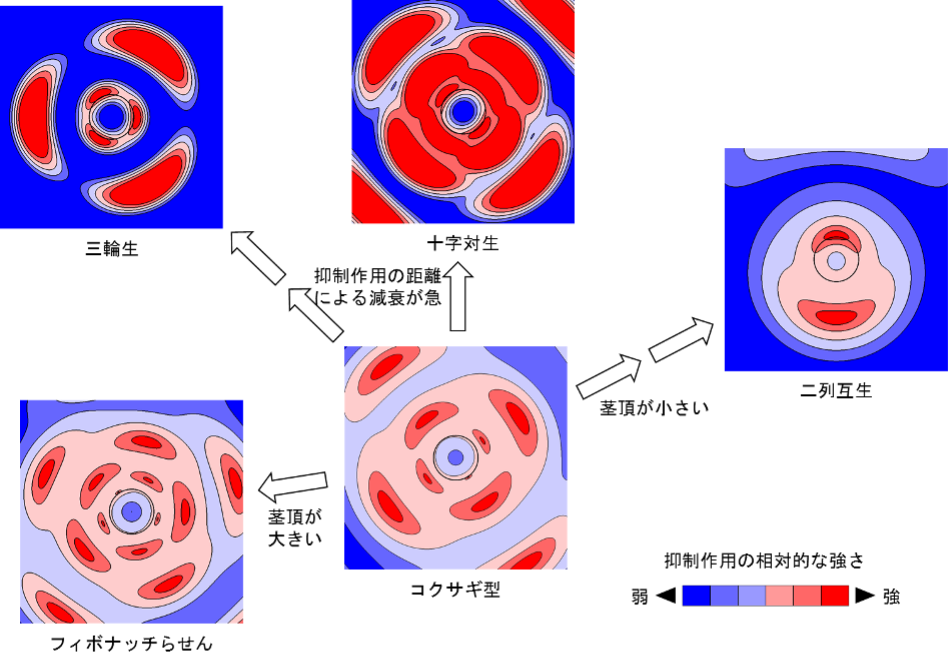
比較的ゆっくりと抑制力が上昇する条件で、EDC2によるコンピュータシミュレーションを行うと、主要な葉序に加えて、コクサギ型葉序も生成された。各パネルは、茎頂を上から見た形で、抑制作用の等高線図として葉序パターンを示している。
EDC2はまた、葉序の頻度分布に関しても、従来のモデルより現実をよく反映していることが判明しました。実際の植物ではらせん葉序の大部分は黄金角に近い開度をもちますが、従来のモデルによるシミュレーションでは180°と黄金角の中間の開度をもつらせん葉序も生じやすく、黄金角の圧倒的優越が十分に説明できていませんでした。これに対し、EDC2のパラメータ空間では中間開度の領域が相対的に狭まり、黄金角近傍の開度の領域が拡がって、黄金角の優越度が大きく増したのです。これらの結果は、EDC2の妥当性を支持し、原基齢依存的な抑制力の上昇がコクサギ型葉序の場合に限られるのではなく、広く一般の植物に共通することを示唆しています。
本研究で得られた知見は、葉原基発生制御における原基間作用の時間変化の重要性を示すとともに、葉序パターンの本質の解明に寄与するものと言えます。将来は、こうした研究の積み重ねにより、自然が織りなす様々な美しい幾何学的パターンを、生成原理から理解できるようになると期待されます。
用語解説:
注1 原基
形成初期の器官で未熟、未発達の状態にあるもの。葉の原基は葉原基と呼ぶ。
注2 葉序
茎を取り巻く葉の配列様式。
注3 コクサギ型葉序
1つの節に葉が1枚ずつ着くタイプの葉序を互生という。コクサギ型葉序は互生の一形式で、コクサギなどに見られる。葉の生じる方向が、0°、180°、270°、90°、0°、……と規則正しく周期的に変わるのが特徴。開度で言うと、180°→90°→180°→270°と変化する。直立していない枝では、左、左、右、右、……というように、左右に2枚ずつ葉が着いているように見えることが多いが、これは葉柄のねじれによる。
注4 分裂組織
細胞分裂を持続的に行って、植物の器官の成長にはたらく組織。茎の先端にあるものは、茎頂分裂組織またはシュート頂分裂組織と呼ばれる。
注5 らせん対称
軸を中心にした回転と軸に沿った並進の合成で、移動後の構造が元の構造と重なるとき、らせん対称という。
注6 二列互生
互生葉序の中で、節ごとに葉が真向かいの位置に互い違いに着くものを二列互生と呼ぶ。開度は180°である。
注7 フィボナッチらせん
連続2項の和が次の項を与えるような数列で、最初の2項が1のものをフィボナッチ数列という(1, 1, 2, 3, 5, 8, 13, ……と続く)。開度が黄金角に近い互生葉序は、フィボナッチ数列と密接に関連する、美しいらせんを描くので、フィボナッチらせんと呼ばれる。
注8 開度
ある葉と次の葉が茎を中心にしてなす角度のこと。
注9 黄金角
円を、全円周と長い弧の長さの比が、長い弧と短い弧の長さの比と等しくなるように二分したとき、つまり黄金比で二分したときの、短い方の弧の中心角。約137.5°。
注10 十字対生
1つの節に2枚の葉が対向するように着く葉序を対生という。ふつう対生葉序では、葉の対の方向が、節ごとに90°ずつ変わる。これを十字対生という。
注11 三輪生
1つの節に3枚の葉が着く葉序。ふつう3枚の葉は等角度、つまり120°の間隔で着き、この3枚の組が節ごとに60°回転する。
注12 パラメータ空間
モデルのパラメータの設定値を座標とする空間。EDC2の場合、パラメータは5つあるので、5次元空間となる。本研究では、この空間に各パラメータ条件で出力された葉序のパターンを位置づけて、その分布から様々な葉序の生じやすさや安定性、相互の関係などを考察した。
論文情報:
雑誌名:「PLOS Computational Biology」(オンライン版:2019年6月6日)
論文タイトル:Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis
著者:Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama

